Introduction
Epilepsy is a fairly common disease (ranked 3rd after stroke and Alzheimer's disease) in the general population, affecting 1-3% of people [1-3]. The true prevalence of epilepsy is unknown and virtually impossible to estimate. In Republic of Moldova, according to data from the National Bureau of Statistics, 60,000 people are diagnosed with epilepsy, of which 13,500-15,000 are women [4]. Correspondingly, the estimated prevalence of epilepsy in Republic of Moldova is 16-19 persons per 1000 population (2015) [5]. As the disease is a stigmatizing one, especially in relation to women, epilepsy becomes an important public health and medico-social problem.
One of the most common requests from patients and their relatives in medical consultations is to provide an answer regarding the outcome and/or prognosis (chance of cure, recurrence, duration, likelihood of complications, success of the treatment, etc.). In order to give a plausible answer, doctors either rely on their own experience, on literature data, or apply various estimation and forecasting tools (scores, nomograms, mathematical models).
The limitations of each of the outcome prediction methods is different - from empirical estimation (intuition of the outcome), with 50/50 probability of error vs. success, based on practical experience, to a population approximation (based on probabilistic scores and models). Unfortunately, none of the methods, no matter how sophisticated, is able to provide a personalized prognosis of what the patient requires.
A compromise option would be to use probabilistic prediction models, based on clinical, instrumental and laboratory indicators, developed using logistic regression. The logistic regression method allows the likelihood of an event to be predicted, based in particular on binary events (presence or absence of crisis, abandonment or not of treatment, etc.). Among the advantages of using logistic regression in the present research are the ease of implementation, interpretation, and sufficient clinical accuracy, given simple and easily obtained parameters. Among the disadvantages should be mentioned the assumption of a linear relationship between the independent variable (the sought outcome) and the dependent variable(s) (which in the real world is not always linear) and the problem of (multi)collinearity. Contemporary statistical tools, however, allow the impact of these shortcomings to be minimized [6-8]. Treatment-resistant epilepsy is defined as the therapeutic failure of two or more antiepileptic drugs, correctly chosen and administered in appropriate doses, depending on the form of epilepsy. The mechanisms of this resistance are either pharmacogenetics in origin, the consequence of neuroplasticity following disease progression, or the consequences of the seizures themselves (e.g., hippocampal sclerosis).
About 7% to 20% of children with epilepsy have developed resistance to anti-epileptic drugs. Meanwhile, 30% to 40% of adult patients remain refractory to drug treatment. Numerous studies have touched on predictors associated with medical resistance in both children and adults. Confirmed risk factors for drug resistance are: early onset of the disorder, abnormal EEG findings and neurological deficit or mental retardation at the time of diagnosis, symptomatic etiology, high seizure frequency and lack of response to first anti-epileptic treatment [9].
In Xue-Ping W.'s (2019) meta-analysis [9] it was found that the prevalence of drug-resistant epilepsy was approximately 27% and the relative risk factors were: abnormal EEG (both slow wave and epileptiform discharges), status epilepticus, symptomatic etiology, febrile seizures and seizures of multiple types, positive outcome to short-term therapy, delayed neurodevelopment, and high frequency of primary seizures. Based on these risk factors, in clinical practice it would be useful for clinicians to predict the course of epilepsy within a short period after diagnosis and to early identify children at risk of intractable epilepsy; this is important both for counselling parents and for clinicians to consider alternative treatments.
However, despite the development of 20 new anticonvulsant drugs since the 1990s, the proportion of patients with drug-resistant epilepsy has remained stable (30%-40%) over the last 30 years. In addition, 80% of patients with epilepsy have been reported to have experienced adverse reactions related to their anticonvulsant medication and 30-40% have reported that adverse effects substantially affected their quality of life or led to discontinuation or non-adherence to medication [10].
The proportion of people with drug-resistant epilepsy has not changed substantially since the 1980s. However, the field of epilepsy has advanced over the last decade and is now entering the era of targeted and precision medicine. Increased understanding of the etiologies of epilepsy, including immune, genetic, and structural causes, has now made it possible, in some patients, to identify specific targets for therapies that go beyond anti-seizure drugs and allow treatment of the cause of epilepsy [10, 11].
Based on the above, the aim of the present study was to develop a predictive mathematical model for the development of antiepileptic medication resistance in women of reproductive age with epilepsy, using the logistic regression and likelihood calculus method, based on 5 years of follow-up of 159 patients.
Methods and materials
The given study is a bidirectional, cohort, descriptive-analytic study. The accumulation of primary material took place during 2016-2020 in the outpatient departments of the Diomid Gherman Institute of Neurology and Neurosurgery, the State Hospital of Republic of Moldova and the Excellence Private Medical Institution, based on bilateral collaboration contracts, signed with each institution, in compliance with bioethical clauses, confidentiality, and protection of personal data and informed consent of patients.
The study protocol was approved by the Research Ethics Committee of the Nicolae Testemiţanu State University of Medicine and Pharmacy (minutes no. 55 of 03.06.2016).
The study subjects were women of reproductive age with epilepsy, where the first epileptic seizure started from birth to 49 years range.
Inclusion criteria were:
women of reproductive age (15-49 years);
signed informed consent;
with no predetermined duration of illness before enrolment, regardless of seizure type;
no comorbidities;
onset of illness - from birth to the end of reproductive age (49 years).
Exclusion criteria were:
refusal of informed consent;
age of patients assessed for enrolment outside the age range 15-49 years;
undocumented or unconfirmed epileptic seizures;
patients with persistent epileptic encephalopathy.
After confirming eligibility and obtaining informed consent, prior to the initiation of the investigation, patients enrolled in the study were informed in detail about the purpose of the study, the requirements, benefits, and risks of the investigations and the treatment administered.
Thus, 159 complete records of patients of reproductive age with epilepsy, who met the inclusion criteria and had none of the exclusion criteria, were included in the final analysis.
All patients enrolled in the study were examined according to the National Clinical Protocol ”Epilepsy in Adults“ and institutional protocols[5].
The clinical examination included the recording of patient data - medical history with epidemiological and demographic data: age, residence, profession (working conditions), level of education (studies), medical history - personal and hereditary medical history (presence of epilepsy in first and second degree relatives), vicious habits, sexual history (menarche, menstrual cycle characteristics, obstetrical and gynecological history, sexual activity and menopause). Objective general clinical examination and neurological examination was performed. Patients were examined by standard clinical methods to assess general condition and neurological status. General and focal neurological symptoms, possible psychiatric, cognitive disorders were identified and entered into the standardized data recording form.
In order to clarify certain events, with the consent of the patients, their relatives and eyewitnesses of the seizures were interviewed. The technique of guided interview questions was applied.
Patients also completed a seizure diary (paper format), which described the symptomatic nature of the seizure, frequency and duration, aura and post seizure signs, time of onset and triggers. This data were then transcribed into the standardized data recording form. Disease- and patient-specific variables with epilepsy were collected a priori, based on the individual and clinical characteristics of each patient. Information about clinical events accompanied by loss of consciousness, amnesia, confusion was assessed based on family and witness information and no objective screening tool was applied to the subjects of the present study.
Before starting the collection of primary material, the number of patients required for enrolment in the study (sample size) was estimated, which would allow confirmation or rejection of the null hypothesis. Thus, the required number of patients was calculated using the free online software GPower 3.1 [12].
Since the main outcome parameters of the study are categorical, with non-Gaussian (non-normal) distribution, and the number of data series was 4 (according to the number of visits), the Kruskal Wallis Test was selected for calculation.
The following calculation steps have been carried out in the Gpower 3.1 software (1) Selected F tests from the Test family menu; (2) Selected ANOVA: fixed effects, omnibus, one way from Statistical test; (3) Selected A priori from power analysis.
Background information was entered: 95% confidence interval for significance of the results, minimum statistical power - 80%; difference of result f = 0.25; number of groups n = 3; number ratio between data series - 1:1.
Calculation results: non centrality parameter (describing the degree of difference between H1 and H0 values) λ = 9.94, critical F-value = 3.05, numerator of degrees of freedom df = 3 (because the calculation was performed based on 4 data series), denominator of degrees of freedom df = 156. Total number of patients required for research = 159.
Regarding the collected parameters, as criteria for their non-inclusion in the logistic regression analysis and the construction of the predictive model for the onset of antiepileptic drug resistance were established: (1) parameters with many individual data missing or having low variability over time; (2) parameters that are in close correlation with others, to avoid collinearity effect problems; (3) parameters that showed insufficient statistical significance (p ≥ 0.2) in univariate analysis.
Finally, for the creation and testing of variants of the antiepileptic drug resistance prediction model, the following parameters were selected (with consideration of the conditions stated above): age at onset of illness (by age categories, at 10, 20 and 30 years), drop-out or poor adherence to prescribed antiepileptic treatment, presence of a brain lesion on brain MRI scan, prolonged confusion after an epileptic seizure (postictal sign), focal activity on electroencephalography without seizure symptoms, anxiety; depression, seizure duration over 6 minutes, status epilepticus occurrence, seizure frequency (discrete quantitative variable).
Since the selected variables were found to be binary categorical, ordinal (with a small ordinal number), or discrete quantitative, the best-fitting predictive models were developed based on multivariate analysis (multiple logistic regression).
The calculation of the probability of occurrence of an event, in models based on logistic regression analysis was done according to formula (1):
![]()
where,
β0: the mean value of the response variable (the interceptor) when X = 0;
β1: the average change in the response variable (constant) for a one unit increase in X;
X: value for the predictor variable (in this case, the clinical sign).
For each model version, the final number of remaining parameters were selected according to the results of the collinearity test, the variance inflation factor (VIF) and the Akaike informativeness criteria. All analysis was performed with the help of Graph Pad Prism software, version 9 trial. For practical convenience, the same results were also reflected by Odds ratios (OR).
Results
The general description of the patients enrolled in the study in terms of age, level of education, living environment, socio-familial status, etc., is presented in Table 1. These characteristics will define the profile of patients of reproductive age with epilepsy for whom the predictive model for the onset of antiepileptic drug resistance is constructed.
Table 1. The general description of the patients enrolled in the study. | |
Parameters | All patients (n = 159) |
Age of onset of the disease, years | 14.0±6.3 [2-34] |
Age of first referral to a neurologist, years | 24.0±7.2 [2-46] |
Level of education
|
4 (2.5%) 100 (62.3%) 56 (35.2%) |
Living environment
|
84 (52.8%) 75 (47.2%) |
Family status
|
109 (68.6%) 45 (28.3%) 5 (3.1%) 0 (0.0%) |
Social class
|
83 (52.3%) 61 (38,3%) 15 (9.4%) |
Vulnerabilities
|
12 (7.6%) 11 (6.9%) |
|
40 (25.2%) 33 (20.8%) |
Note: Age data are expressed as mean and standard deviation, with extreme values presented. * - patients with official unemployment status; ** - patients with disability status, granted by the National Disability Determination Council of the Republic of Moldova. Data are presented as mean and standard deviation [extremes] or as absolute (relative) values. | |
The results of logistic regression of the parameters that met the eligibility criteria (anxiety, depressed state, brain structural abnormality on MRI image, discontinuation of antiepileptic treatment, epileptic seizure lasting more than 6 minutes, confusional state after epileptic seizure, status epilepticus, and frequency of epileptic seizures) are presented in Table 2. Of note, the parameters in Table 2 do not show collinearity with each other because the variance inflation factor, VIF ≤2, R2à0.
Table 2. Multiple logistic regression parameters for the onset over time of patients' antiepileptic drug resistance calculated according to the clinical indicators proven to be relevant. | |||||
Parameters | β (SE) | OR (95CI) | VIF | R2 | Mean Probability |
Interceptor (β0) | 0.78 (0.34) | 2.19 (1.13 – 4.32) | - | - | 69% |
A (β1) | 0.06 (0.24) | 1.06 (0.67 – 1.70) | 1.046 | 0.04 | 52% |
B (β2) | 0.75 (0.26) | 2.11 (1.2 – 3.50) | 1.066 | 0.06 | 68% |
C (β3) | 0.68 (0.26) | 1.97 (1.20 – 3.30) | 1.095 | 0.09 | 66% |
D (β4) | -0.34 (0.25) | 0.71 (0.43 – 1.17) | 1.075 | 0.07 | 42% |
E (β5) | 0.24 (0.25) | 1.28 (0.78 – 2.08) | 1.127 | 0.11 | 56% |
F (β6) | -0.43 (0.77) | 0.65 (0.15 – 3.42) | 1.039 | 0.04 | 39% |
G (β7) | 0.16 (0.25) | 1.17 (0.71 – 1.91) | 1.049 | 0.05 | 54% |
H (β8) | -0.001 (0.001) | 0.99 (0.99-1.00) | 1.068 | 0.06 | 50% |
“Nota:”: A - anxiety; B - depression; C - brain structural abnormality on MRI image; D - drop-out of antiepileptic treatment; E - epileptic seizure lasting more than 6 minutes; F - status epilepticus; G - confusional state after epileptic seizure; - annual frequency of epileptic seizures; VIF - variance inflation factor; R2 - multiple correlation coefficient. | |||||
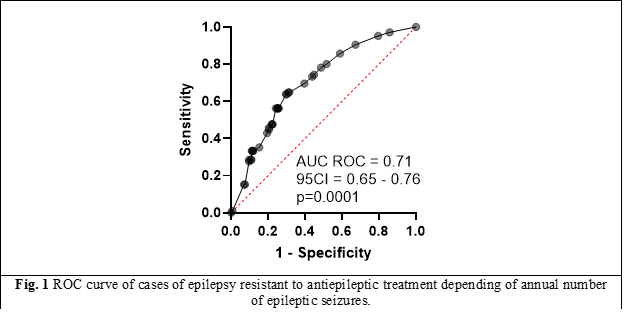
Of all the parameters mentioned in Table 2, only “annual frequency of epileptic seizures” is a discrete quantitative parameter. As the number of observations increases, it tends to have a normal (Gaussian) distribution and behaves as a continuous quantitative parameter. In this respect, it was examined whether a cut-off value could be identified, which would allow a more accurate prediction (with clinically acceptable sensitivity and specificity) of the onset of resistance to antiepileptic drug treatment. Respectively, figure 1 shows the ROC curve of antiepileptic drug-resistant epilepsy cases (from the study group) versus annual seizure frequency. Although it is clearly shown that increased frequency of epileptic seizures is one of the relevant clinical indicators (AUC = 0.71; 95CI: 0.65 - 0.76; p=0.0001) of the onset of resistance to antiepileptic treatment, an exact cut-off value in this respect is impossible to define (identify).
Figure 2 reflects the interrelationship between the likelihood of developing epilepsy resistant to antiepileptic treatments and the annual frequency of epileptic seizures, where the trend is evident. This finding leads to the conclusion that in a probabilistic model for predicting the development of antiepileptic drug resistance over time, seizure frequency must necessarily be part of the model.
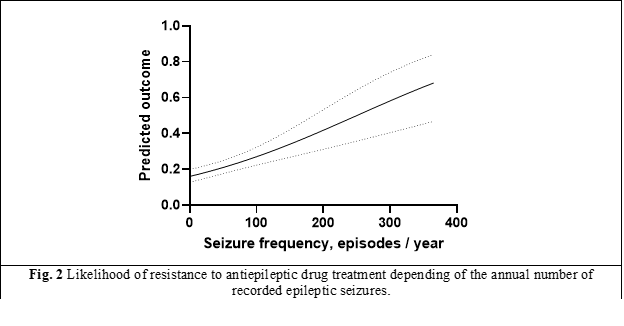
From figure 2, for practical guidance - a number of 20 epileptic seizures per month, for 2 consecutive months (according to the following calculations: 250 seizures per year with 50% average probability of resistance installed / 52 weeks of the year = 5 epileptic seizures per week), against the background of correct treatment, as drug combination and appropriate dosage, will indicate a high probability of antiepileptic drug resistant epilepsy. It should be noted that in this case, other concurrent symptoms (depression, anxiety, post-seizure symptoms), which increase the probability of antiepileptic drug resistance, were not taken into account, but only the epileptic seizure itself as an on event (unspecified, however, in duration and intensity).
Based the parameters described in table 2, it is possible to develop several prediction models, based on multiple logistic regression, by summing the individual contribution of each parameter to the final characteristics of the model, with or without taking into account the influences produced by the interaction between variables.
Table 3. A comparison of two multiple logistic regression models for the onset of resistance to EC treatment over time, calculated on the basis of clinical indicators with significant odds ratios. | ||||
Parameters | Model rez_1 | Model rez_2 | ||
β (SE) | OR (95CI) | β (SE) | OR (95CI) | |
Interceptor (β0) | 1.16 (0.97) | 3.2 (0.5 – 24.2) | 0.99 (0.86) | 2.68 (0.52 – 16.37) |
A (β1) | 0.10 (0.25) | 1.1 (0.7 – 1.8) | 0.11 (0.25) | 1.12 (0.69 – 1.82) |
B (β2) | -0.21 (0.65) | 0.8 (0.2 – 2.9) | 0.22 (0.54) | 1.24 (0.42 – 3.55) |
C (β3) | -0.91 (0.79) | 0.4 (0.1 – 1.9) | -1.14 (0.72) | 0.31 (0.08 – 1.33) |
D (β4) | -0.48 (0.67) | 0.6 (0.2 – 2.3) | -0.35 (0.26) | 0.70 (0.41 – 1.16) |
E (β5) | 0.20 (0.72) | 1.2 (0.3 – 5.3) | 0.23 (0.62) | 1.26 (0.37 – 4.34) |
F (β6) | 0.45 (0.77) | 1.6 (0.3 – 6.8) | 0.47 (0.77) | 1.60 (0.31 – 6.85) |
G (β7) | 0.23 (0.68) | 1.3 (0.3 – 4.8) | 0.01 (0.55) | 1.01 (0.34 – 2.99) |
H (β8) | -0.01 (0.002) | 0.9 (0.8 – 1.0) | -0.01 (0.002) | 0.98 (0.96 – 0.99) |
B + C (β9) | 0.74 (0.66) | 2.1 (0.5 – 7.5) | 0.74 (0.64) | 2.10 (0.58 – 7.30) |
B + D (β10) | 0.77 (0.59) | 2.2 (0.7 – 7.1) | - | - |
B + E (β11) | 0.12 (0.60) | 1.1 (0.3 – 3.7) | 0.17 (0.59) | 1.19 (0.38 – 3.80) |
B + G (β12) | 0.13 (0.67) | 1.1 (0.30 – 4.2) | 0.23 (0.65) | 1.27 (0.35 – 4.57) |
C + D (β13) | -0.42 (0.58) | 0.6 (0.2 – 2.0) | - | - |
C + E (β14) | 0.50 (0.57) | 1.6 (0.5 – 4.9) | 0.47 (0.56) | 1.60 (0.53 – 4.81) |
C + G (β15) | 1.19 (0.67) | 3.3 (0.8 – 12.4) | 1.16 (0.65) | 3.17 (0.89 – 11.55) |
D + E (β16) | -0.06 (0.53) | 0.9 (0.3 – 2.7) | - | - |
D + G (β17) | -0.37 (0.57) | 0.7 (0.2 – 2.1) | - | - |
E + G (β18) | -0.55 (0.54) | 0.6 (0.2 – 1.6) | -0.66 (0.53) | 0.52 (0.18 – 1.43) |
B + C + H (β19) | 0.01 (0.005) | 1.0 (1.0 – 1.1) | 0.01 (0.005) | 1.01 (1.00 – 1.03) |
B + G + H (β20) | 0.001 (0.004) | 1.0 (0.9 – 1.0) | 0.001 (0.004) | 1.00 (0.99 – 1.01) |
C + G + H (β21) | -0.006 (0.007) | 0.9 (0.9 – 1.0) | -0.007 (0.007) | 0.99 (0.98 – 1.01) |
AICc (β0) | 512.0 | 513.0 | ||
AICc of the model | 492.0 | 486.0 | ||
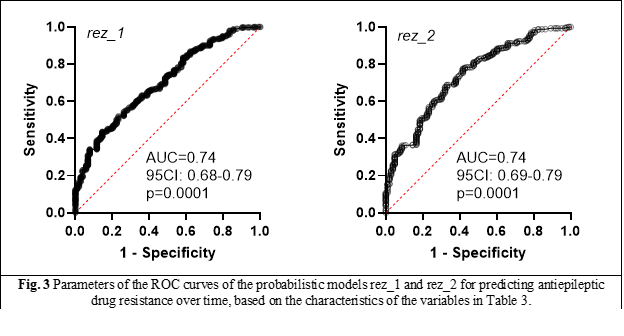
AUC ROC | 0.74 (0.69 – 0.79) | 0.74 (0.68 – 0.79) | ||
PPN, % | 62% | 59% | ||
PPP, % | 83% | 83% | ||
Probability, % | 96% | 96% | ||
“Nota:” A - anxiety; B - depression; C - brain lesion on MRI examination; D - discontinuation of antiepileptic treatment; E - epileptic seizure lasting 6 minutes or more; F - epileptic status; G - confusional state after epileptic seizure; H - seizure frequency; AICc - Akaike informativeness criterion. | ||||
Table 3 presents the characteristics of two probabilistic prototype models, named rez_1 and rez_2, which also take into account the contribution of interaction effects between 2 and 3 variables, in addition to the individual contribution of each model parameter to its summary predictive ability. Model rez_2 differs from model rez_1 in that the contributions of interaction effects between B-D (depression, drop-out of antiepileptic treatment), C-D (MRI brain lesion and drop-out of antiepileptic treatment), D-E (drop-out of antiepileptic treatment and seizure lasting more than 6 min) and D-G (drop-out of antiepileptic treatment and confusional state after seizure) were not included.
Both models (rez_1 and rez_2) possess absolutely similar performance characteristics (AUC ROC, PPN, PPP, likelihood) (Figure 3). At the same time, the Akaike informativeness criterion points to a low contribution to the final characteristics of the models of interactions between 2 and 3 variables, which means that they can be omitted from the calculations, with the deduction of a simpler predictive model.
After simplification, the AErez model is the “successor” of models rez_1 and rez_2, which was developed with consideration of the findings made based on the information in Table 3. A mandatory parameter in the model was the annual frequency of epileptic seizures. A frequency of 20 or more epileptic seizures per month was proposed, somewhat empirically, as a condition for including the variable in the model. Thus, the AErez model is presented in formula (2 and 3).
So, according to the AErez model, patients with epilepsy who suffer from depression and have a brain lesion on MRI imaging, who have, for example, 20 or more epileptic seizures per week, have an 84% probability of developing a treatment-resistant form of epilepsy. In other words, patients who have all of the above characteristics will have at least (0.84 / 1-0.84) 5.3 times more frequent treatment-resistant epilepsy than patients who do not have these characteristics.
Discussions
A PubMed search on predictive models (of any kind) in epilepsy (any category), covering the period 1975-2022, returned 2821 results based on the keywords “predictive models”, “outcome prediction”, “epilepsy”. An exponential increase in the number of publications selected by the search engine based on these keywords began to emerge after 2010 (86 publications per year), reaching 355 publications in 2022. A search by restriction criteria (articles in extenso, published between the years 2012-2022, in English, that directly address the topic of predictive models in epilepsy), led to a final list of 25 publications, which have been analyzed and systematized in this section.
In adults, the rate of resistance is about 4% per year. In the study group, the rate of resistance, expressed as the total number of episodes observed during the 4 visits, was 107 episodes per 462 patient-visits (23.1%), which is an extremely high rate. In this context, the identification of clinical predictors, framed in a mathematical model, is particularly motivating and important.
Prediction models have long been used as clinical decision support (CDS) tools in medical practice. CDS is a complex term that encompasses a variety of tools designed to assist clinicians in their workflow and improve patient outcomes. Established examples include alert systems, computerized ECG interpretation, automated dose adjustment assistance for patients with renal failure, diagnostic tools, and models that can aid decision making (e.g., medication choice) and outcome prediction [13]. However, the data revolution in medicine and science is spurring increased interest in CDS and personalized prediction.
Unlike traditional approaches, which rely on the assumption of a data model, algorithms developed by machine learning (ML) models are retrieved directly from data [14].
Examples of ML models include decision trees (a decision tree is a type of supervised machine learning used to classify or make predictions based on how a previous set of questions was answered; the model is a form of supervised learning, meaning that the model is trained and tested on a data set containing the desired categorization), support vector machine (SVM), k-nearest neighbor algorithm, random forests study method, artificial neural networks, and K-means. Machine learning models are divided into supervised learning and unsupervised learning. Supervised learning involves "training" ML algorithms on datasets consisting of inputs (or features) and "labeling" outputs. Unsupervised learning does not use labeled data, but attempts to extract underlying patterns from a dataset [13]. To calculate prognosis, numerical values are often simplified as categorical variables, and the weight given to predictive factors is rounded to integers and only a limited subset of variables can be included in the prognostic index. ML is a branch of artificial intelligence, which is entering the clinical research field at an increasing pace. ML allows digital algorithms to learn from experience without being explicitly programmed to do so [15].
In the study by Lamberink H. (2017) [16], it was outlined that the strongest predictors included in nomograms for crisis recurrence were: duration of epilepsy, duration of seizure-free interval, age at seizure onset, history of febrile seizures, ten or more seizures before remission, absence of a self-limited epilepsy syndrome (such as, absence or Rolandic epilepsy, or Panayiotopoulos syndrome), intelligence quotient (IQ) below 70, and epileptiform abnormality on EEG before discontinuation of antiepileptic drugs. To predict long-term seizure outcome, the eight independent predictors selected were: duration of epilepsy, duration of seizure-free interval, number of antiepileptic drugs before discontinuation, female gender, family history of epilepsy in first- or second-degree relatives, ten or more seizures before remission, presence of focal seizures, and epileptiform abnormality on EEG before discontinuation of antiepileptic drugs. Validation, or assessing how well a prediction works on data other than that on which the model was built, is arguably the most important issue in prognostic modelling.
Comparing with accessible scientific evidence, it was found that a number of common parameters were found in the own models developed, reported by a number of authors - namely, (early) age, drop-out from antiepileptic treatments, EEG abnormalities, structural abnormalities on MRI. However, the investigated cohort (patients of reproductive age) has not been mentioned in predictive models in the literature. Also, for the first time, attention was paid to depression - a symptom frequently encountered in reproductive age patients with epilepsy, which contributes significantly to the increased likelihood of an adverse outcome scenario.
Finally, it is found that in predictive models, based on clinical indicators (“categorical data”), taking into account the contribution to accuracy of the interactions between 2 and/or 3 parameters, added to the contribution given by the sum of the results of the individual variables is not so relevant for clinical practice, brings unnecessary complexity and decreases the clinical practice adoption medical practitioners. It is therefore recommended to use the developed simplified models.
Future studies are needed to build a model that is applicable to a wider range of patients with epilepsy, which will provide an easier, faster and more reliable method to predict the risk of antiepileptic drug resistance.
Conclusions
The predictive model developed (AErez), based on 3 parameters (depressive state, annual frequency of seizures, presence of brain lesions on MRI) has a positive predictive value of 83%, negative of 62%, with an area under the ROC curve of 0.72 (95%CI = 0.56 to 0.88) and a probability of event occurrence of 96%. Depressed patients with documented structural lesions on MRI and a high frequency of epileptic seizures have a progressive, significant (5.3-24.0-fold) risk of developing resistance to antiepileptic drugs.
Competing interests
None declared.
Authors’ contribution
VC conceived conceptualization, methodology, data collection, analysis and interpretation, writing - original draft preparation. MG conceived writing review and editing, supervision, funding acquisition, validation. The authors read and approved the final version of the manuscript.
Patient consent
Obtained.
Funding statement
The authors report no financial support.
Ethics approval
The study protocol was approved by the Research Ethics Committee of Nicolae Testemiţanu State University of Medicine and Pharmacy (minutes no. 55 of 03.06.2016).
Author’s ORCID IDs
Victoria Duca – https://orcid.org/0000-0003-2147-9359
Mihail Gavriliuc - https://orcid.org/0000-0002-5789-2842
References
Forsgren L, Beghi E, Oun A, Sillanpää M. The epidemiology of epilepsy in Europe – a systematic review. Eur J Neurol. 2005 Apr;12(4):245-253. doi: 10.1111/j.1468-1331.2004.00992.x.
Sander J. The epidemiology of epilepsy revisited. Curr Opin Neurol. 2003 Apr;16(2):165-70. doi: 10.1097/01.wco.0000063766.15877.8e.
Banerjee P, Filippi D, Hauser W. The descriptive epidemiology of epilepsy – a review. Epilepsy Res. 2009 Jul;85(1):31-45. doi: 10.1016/j.eplepsyres.2009.03.003.
National Bureau of Statistics of the Republic of Moldova [Internet]. Chisinau: The Bureau; 2023- [cited 2022 June 6]. Available from: https://statistica.gov.md/ro.
Groppa S, Chiosa V, Cobileanschi O, et al.; Ministry of Health of the Republic of Moldova. [Epilepsy in adults: National Clinical Protocol: NCP-290] [Internet]. Chisinau: The Ministry; 2017. 46 p. Romanian. [cited 2023 May 13]. Available from: https://repository.usmf.md/bitstream/20.500.12710/10670/1/Epilepsia_la_adult_Protocol_clinic_national_PCN_290.pdf
Vittinghof E, Glidden D, Shibovschi S, Mcculloch C. Regression methods in biostatistics: linear, logistic, survival, and repeated measures models. 2nd ed. New York: Springer; 2012. 509 p. (Statistics for Biology and Health).
James G, Wittwn D, Hastie T, Tibshirani R. An introduction to statistical learning: with applications in R. New York: Springer; 2013.
Johnston R, Jones K, Manley D. Confounding and collinearity in regression analysis: a cautionary table and an alternative procedure, illustrated by studies of British voting behaviour. Qual Quant, 2018;52(4):1957-1976. doi: 10.1007/s11135-017-0584-6.
Xue-Ping W, Hai-Jiao W, Li-Na Z, Xu D, Ling L. Risk factors for drug-resistant epilepsy: a systematic review and meta-analysis. Medicine (Baltimore) 2019 Jul;98(30):e16402. doi: 10.1097/MD.0000000000016402.
Kovács R, Heinemann U. Models in research of pharmacoresistant epilepsy: present and future in development of antiepileptic drugs. Curr Med Chem. 2014;21(6):689-703. doi: 10.2174/0929867320666131119152613.
Yang W, Zhang X, Long J, Wu Q, Han Y. Prediction of the recurrence risk in patients with epilepsy after the withdrawal of antiepileptic drugs. Epilepsy Behav. 2020 Sep;110:107156. doi: 10.1016/j.yebeh.2020.107156.
Faul F, Erdfelder E, Lang A, Buchner A. G*Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav Res Methods. 2007;39(2): 175-191. doi: 10.3758/bf03193146.
Smolyansky E, Hakeem H, Ge Z, Chen Z, Kwan P. Machine learning models for decision support in epilepsy management: a critical review. Epilepsy Behav. 2021;123:108273. doi: 10.1016/j.yebeh.2021.108273.
Alim-Marvasti A, Vakharia V, Duncan J. Multimodal prognostic features of seizure freedom in epilepsy surgery. J Neurol Neurosurg Psychiatry. 2022 May;93(5):499-508. doi: 10.1136/jnnp-2021-327119.
Senders J, Staples P, Karhade A, Zaki M, et al. Machine learning and neurosurgical outcome prediction: a systematic review. World Neurosurg. 2018 Jan;109:476-486.e1. doi: 10.1016/j.wneu.2017.09.149.
Lamberink H, Otte W, Geerts A, Pavlovic M, et al. Individualised prediction model of seizure recurrence and long-term outcomes after withdrawal of antiepileptic drugs in seizure-free patients: a systematic review and individual participant data meta-analysis. Lancet Neurol. 2017 Jul;16(7):523-531. doi: 10.1016/S1474-4422(17)30114-X